フィルタの構成方法と適用方法について記録を残す。MATLAB-STYLE IIR Filterから。
リファレンスはここにある。
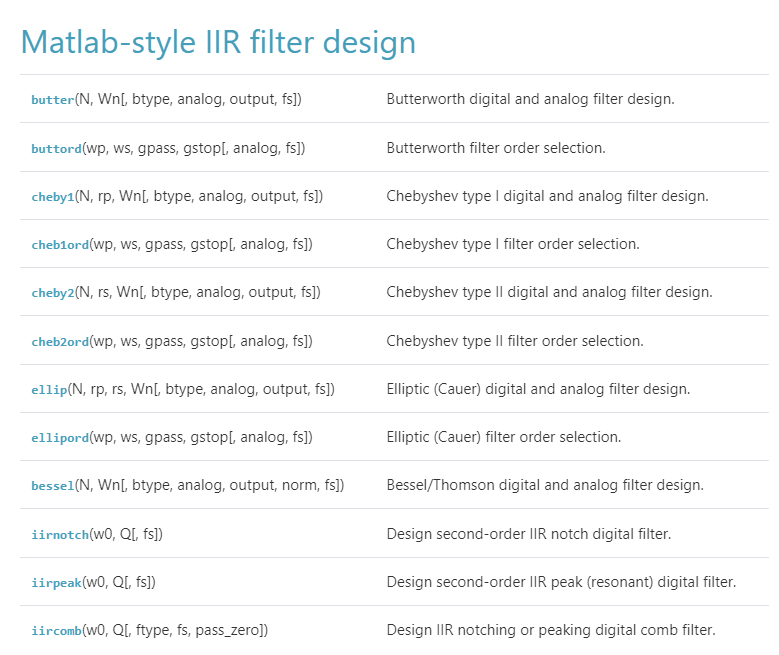
まぁ、まずは動くところを確認しよう。
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
twopi=2*np.pi
f_sampling_simulation=1e9
f_center=500e3
q_value=10
zeta=1/(2*q_value)
fcut=np.array([f_center-zeta*f_center,f_center+zeta*f_center])
print(fcut)
wcut=fcut/(f_sampling_simulation/2)
b,a=signal.butter(1,wcut,'bandpass')
w,h=signal.freqz(b,a,worN=2**20)
freqs=w*f_sampling_simulation/twopi
h_abs=np.abs(h)
#amp_max=np.max(h_abs)
#amps_db=20*np.log10(h_abs/amp_max)
amps_db=20*np.log10(h_abs)
angles=np.angle(h)*180/np.pi
fig = plt.figure()
ax1=plt.subplot(1,1,1)
ax1.grid(True)
ax1.plot(freqs,amps_db, '-')
ax1.set_xlim(400e3,600e3)
ax1.set_ylim(-50,0)
ax1.set_ylabel('Amplitude [dB]')
ax2=ax1.twinx()
ax2.grid(True)
ax2.plot(freqs,angles, 'r-')
ax2.set_xlim(0,1e6)
ax2.set_ylim(-180,180)
ax2.set_yticks(np.arange(-180,181,step=90))
ax2.set_xlabel('frequency [Hz]')
ax2.set_ylabel('Phase [deg.]')
fig.tight_layout()
plt.show()
あとで、実際にフィルタをかけることを考慮して、サンプリング周波数を1GHzとしています。そすと、freqz(周波数レスポンスを計算してくれる便利なやつ)の計算が粗くなって低周波の計算をしてくれないので、freqzのオプションworNを大きな値にしています。
で、
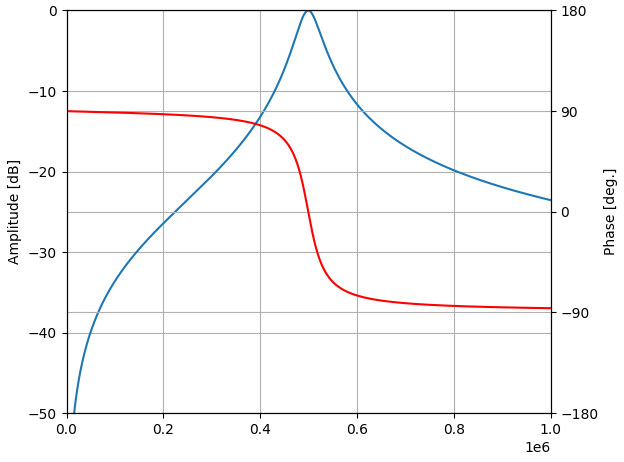
こうなる。
では、ASK変調波形にフィルタを適用してみよう。フィルタをかける便利なやつはlfilterです。ASK変調波形はASK変調のスペクトル(3)で使ったコードを再利用して生成します。
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
# よく使う変数
pi=np.pi
deg2rad=pi/180.0
rad2deg=180.0/pi
twopi=2*pi
# シンボル列を引き延ばす
def extend_symbol_to_simulation_sampling_rate(symbols,t_symbol,t_simulation_sampling):
# シンボル数
size_of_symbols=symbols.size
# 最後のシンボルが終わる時間
end_time=size_of_symbols*t_symbol
# 計算タイミング
t=np.arange(0,end_time,t_simulation_sampling)
# 各シンボルの開始(終了)時間
t_periods_of_symbols=np.append(0,np.arange(1,size_of_symbols,1)*t_symbol)
# 結果データ領域確保
ex_symbols=np.zeros_like(t)
# 先頭データは入れておく
ex_symbols[0]=symbols[0]
# 各シンボルについて、その期間のインデックスを取得し、データを入れ込む
for i in range(0,size_of_symbols):
ex_symbols[np.where(t>t_periods_of_symbols[i])]=symbols[i]
return ex_symbols,end_time
def generate_ask(f_carrier,f_sym,f_samp_generation,phase_carrier_initial,symbols_in_base):
t_sym=1/f_sym
t_samp_generation=1/f_samp_generation
omega_carrier=twopi*f_carrier
# シンボルを計算用に拡張
[symbols,t_end]=extend_symbol_to_simulation_sampling_rate(symbols_in_base,t_sym,t_samp_generation)
# 計算するタイミング
t=np.arange(0,t_end,t_samp_generation)
# 波形生成
amp_t=np.exp(1j*omega_carrier*t+phase_carrier_initial)*symbols
return t,symbols,amp_t
f_sampling_simulation=1e9
f_carrier=500e3
#generate ask waveform
f_symbol=10e3 # シンボルレート in Hz
t_sampling_simulation=1/f_sampling_simulation
phase_initial=0*deg2rad # 搬送波の初期位相(何でもいい) in rad
symbols_in_base=np.array([1,0,1,0,1,0,1,0,1,0,1,0])
t,baseband_t,amp_t=generate_ask(f_carrier,f_symbol,f_sampling_simulation,phase_initial,symbols_in_base)
amp_t=np.real(amp_t) #現実世界重視のため
number_of_samples=t.size
#フィルタ生成
q_value=10
zeta=1/(2*q_value)
fcut=np.array([f_carrier-zeta*f_carrier,f_carrier+zeta*f_carrier])
print(fcut)
wcut=fcut/(f_sampling_simulation/2)
b,a=signal.butter(1,wcut,'bandpass')
w,h=signal.freqz(b,a,worN=2**20)
freqs=w*f_sampling_simulation/twopi
h_abs=np.abs(h)
amps_db=20*np.log10(h_abs)
angles=np.angle(h)*rad2deg
#フィルタ適用
amp_filtered_t=signal.lfilter(b,a,amp_t)
#プロット
fig = plt.figure()
ax1=plt.subplot(4,1,1)
ax1.grid(True)
ax1.plot(freqs,amps_db, '-')
ax1.set_xlim(400e3,600e3)
ax1.set_ylim(-50,0)
ax1.set_ylabel('Amplitude [dB]')
ax1_2=ax1.twinx()
ax1_2.grid(True)
ax1_2.plot(freqs,angles, 'r-')
ax1_2.set_xlim(0,1e6)
ax1_2.set_ylim(-180,180)
ax1_2.set_yticks(np.arange(-180,181,step=90))
ax1_2.set_xlabel('frequency [Hz]')
ax1_2.set_ylabel('Phase [deg.]')
ax2=plt.subplot(4,1,2)
ax2.plot(t,baseband_t)
ax3=plt.subplot(4,1,3)
ax3.plot(t,amp_t)
ax4=plt.subplot(4,1,4)
ax4.plot(t,amp_filtered_t)
fig.tight_layout()
plt.show()
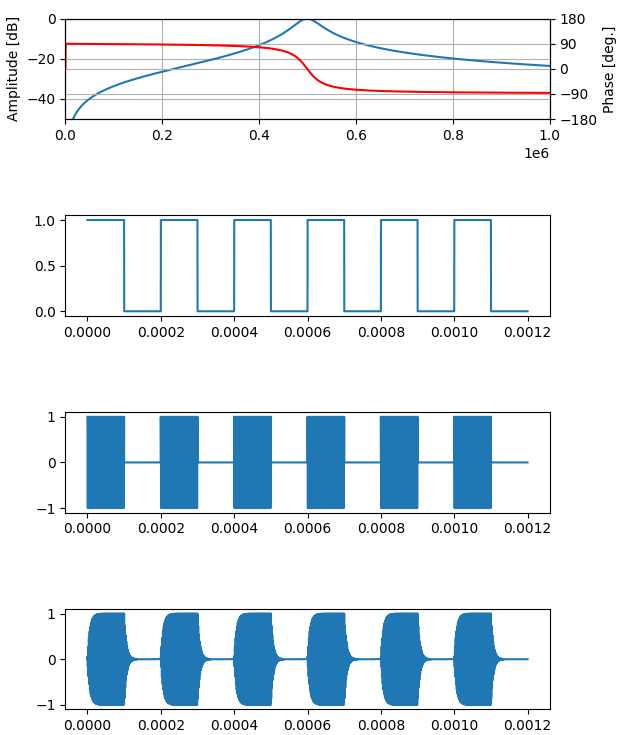
ほらできた。
フィルタで帯域を制限したことで、波形がなまっています。
今日は忙しいのでここまで。

コメントをお書きください