そもそもの式は
\[ f \left( t \right)= a_{0}+\displaystyle \sum_{n=1}^\infty \left\{ a_{n}\cos \left(
\frac{2 \pi n}{T} t \right) + b_{n}\sin \left( \frac{2 \pi n}{T} t \right) \right\} \tag{1} \]

めんどくさいので、答えだけ
\[ a_0=\frac{t_p}{T} \tag{2} \]
\[ a_n=\frac{2}{\pi n} \sin \left( \frac{\pi n}{T} t_p \right) \tag{3} \]
\[ f \left( t \right)= \frac{t_p}{T} +\displaystyle \sum_{n=1}^\infty \left\{
\frac{2}{\pi n}\sin\left(\frac{\pi n}{T}t_p\right) \cos \left( \frac{2 \pi n}{T} t \right) \right\} \tag{4} \]
numpyで確認
- # 変数クリア
- from IPython import get_ipython
- get_ipython().magic('reset -sf')
- import matplotlib.pyplot as plt
- import numpy as np
- # よく使う変数
- pi=np.pi
- # 設定
- T=1
- tp=0.001
- repeat_num=20
- # 計算する範囲と刻みで計算ポイントを作る
- t=np.arange(-T,T,0.00001)
- # 式に値を入れて結果を得る
- a=np.zeros(repeat_num)
- f_t=np.zeros((repeat_num,t.size))
- a[0]=tp/T
- f_t[0,:]=np.ones_like(t)*a[0]
- for n in range(1,repeat_num):
- a[n]=2/n/pi*(np.sin(n*pi/T*tp))
- f_t[n,:]=f_t[n-1,:]+a[n]*np.cos(2*pi*n/T*t)
- # プロット
- fig=plt.figure()
- plt.plot(t,f_t[1],label="n=1")
- plt.plot(t,f_t[2],label="n=1,2")
- plt.plot(t,f_t[3],label="n=1,2,3")
- plt.plot(t,f_t[4],label="n=1,2,3,4")
- plt.plot(t,f_t[5],label="n=1,...,5")
- plt.legend()
- fig=plt.figure()
- plt.plot(t,f_t[repeat_num-1],label="n=1,...,"+str(repeat_num))
- plt.legend()



(4)でtの代わりにt-T/4と書けばよい。
答えがきれいにならないので、もうこれ以上やらない。
\[ f \left( t \right)= \frac{t_p}{T} +\displaystyle \sum_{n=1}^\infty \left\{
\frac{2}{\pi n}\sin\left(\frac{\pi n}{T}t_p\right) \cos \left( \frac{2 \pi n}{T} \left(t-\frac{T}{4}\right) \right) \right\} \tag{5} \]
numpyで確認
- # 変数クリア
- from IPython import get_ipython
- get_ipython().magic('reset -sf')
- import matplotlib.pyplot as plt
- import numpy as np
- # よく使う変数
- pi=np.pi
- # 設定
- T=1
- tp=0.001
- repeat_num=20
- # 計算する範囲と刻みで計算ポイントを作る
- t=np.arange(-T,T,0.00001)
- # 式に値を入れて結果を得る
- a=np.zeros(repeat_num)
- f_t=np.zeros((repeat_num,t.size))
- a[0]=tp/T
- f_t[0,:]=np.ones_like(t)*a[0]
- for n in range(1,repeat_num):
- a[n]=2/n/pi*(np.sin(n*pi/T*tp))
- f_t[n,:]=f_t[n-1,:]+a[n]*np.cos(2*pi*n/T*(t-T/4))
- # プロット
- fig=plt.figure()
- plt.plot(t,f_t[1],label="n=1")
- plt.plot(t,f_t[2],label="n=1,2")
- plt.plot(t,f_t[3],label="n=1,2,3")
- plt.plot(t,f_t[4],label="n=1,2,3,4")
- plt.plot(t,f_t[5],label="n=1,...,5")
- plt.legend()
- fig=plt.figure()
- plt.plot(t,f_t[repeat_num-1],label="n=1,...,"+str(repeat_num))
- plt.legend()

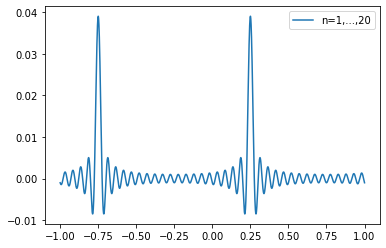
それらしい結果になりました。
で、一番低い周波数成分が、1/Tになっているので、矩形波と同じように、パルスで直交復調してもよいってことでしょ。

コメントをお書きください