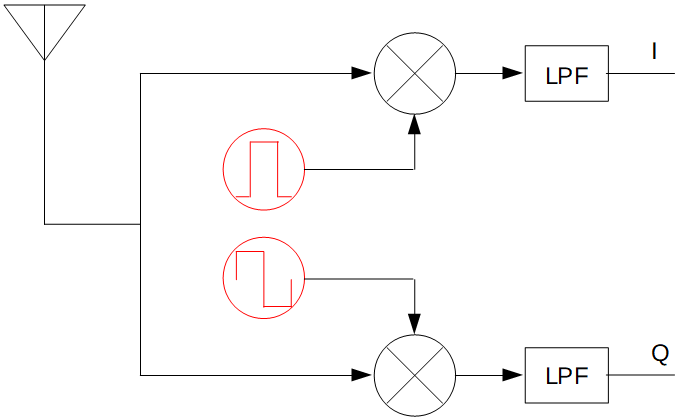
入力信号
\[ S\left(t\right) = A \cos
\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}\right\} \tag{1} \]
局発I
\[ S_{LI} \left( t \right)= \frac{4}{\pi} \displaystyle \sum_{n=1}^\infty \frac {
\left(-1\right)^{n+1} \cos \left\{ \left(2n-1\right) \frac{2 \pi}{T_{L}} t \right\} } {\left(2n-1\right)} \tag{2} \]
局発Q
\[ S_{LQ} \left( t \right)= \frac{4}{\pi} \displaystyle \sum_{n=1}^\infty
\frac{\sin\left\{\left(2n-1\right)\frac{2 \pi}{T_{L}} t\right\}}{2n-1} \tag{3} \]
\[ \omega_{L}=\frac{2 \pi}{T_{L}} \tag{4} \]
とすると、(2)(3)はそれぞれ
\[ S_{LI} \left( t \right)= \frac{4}{\pi} \displaystyle \sum_{n=1}^\infty \frac {
\left(-1\right)^{n+1} \cos \left\{ \left(2n-1\right) \omega_{L} t \right\} } {\left(2n-1\right)} \tag{5} \]
\[ S_{LQ} \left( t \right)= \frac{4}{\pi} \displaystyle \sum_{n=1}^\infty
\frac{\sin\left\{\left(2n-1\right)\omega_{L} t\right\}}{2n-1} \tag{6} \]
(5)(6)を展開するとそれぞれ
\[ S_{LI} \left( t \right)= \frac{4}{\pi}\cos\left(\omega_{L} t\right) -\frac{4}{3
\pi}\cos\left(3 \omega_{L} t\right) +\frac{4}{5 \pi}\cos\left(5 \omega_{L} t\right) -\frac{4}{7 \pi}\cos\left(7 \omega_{L} t\right) +\cdots \tag{7} \]
\[ S_{LQ} \left( t \right)= \frac{4}{\pi}\sin\left(\omega_{L} t\right) +\frac{4}{3
\pi}\sin\left(3 \omega_{L} t\right) +\frac{4}{5 \pi}\sin\left(5 \omega_{L} t\right) +\frac{4}{7 \pi}\sin\left(7 \omega_{L} t\right) +\cdots \tag{8} \]
入力信号にI復調局発を乗ずると、
\[ S_{I} \left( t \right)= A \cos
\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}\right\} \left\{ \frac{4}{\pi}\cos\left(\omega_{L} t\right) -\frac{4}{3 \pi}\cos\left(3 \omega_{L} t\right) +\frac{4}{5
\pi}\cos\left(5 \omega_{L} t\right) -\frac{4}{7 \pi}\cos\left(7 \omega_{L} t\right) +\cdots \right\} \tag{9} \]
\[ \begin{eqnarray} S_{I} \left( t \right)=
\frac{4A}{\pi}\cos\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}\right\}\cos\left(\omega_{L} t\right) \\ -\frac{4A}{3
\pi}\cos\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}\right\}\cos\left(3 \omega_{L} t\right) \\ +\frac{4A}{5
\pi}\cos\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}\right\}\cos\left(5 \omega_{L} t\right) \\ -\frac{4A}{7
\pi}\cos\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}\right\}\cos\left(7 \omega_{L} t\right) +\cdots \end{eqnarray} \tag{10} \]
\[ \begin{eqnarray} S_{I} \left( t \right)=
\frac{2A}{\pi}\cos\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}-\omega_{L}
t\right\}+\frac{2A}{\pi}\cos\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}+\omega_{L} t\right\} \\ -\frac{2A}{3
\pi}\cos\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}-3\omega_{L} t\right\}-\frac{2A}{3 \pi}\cos\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}+3\omega_{L}
t\right\} \\ +\frac{2A}{5 \pi}\cos\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}-5\omega_{L} t\right\}+\frac{2A}{5
\pi}\cos\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}+5\omega_{L} t\right\} \\ -\frac{2A}{7
\pi}\cos\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}-7\omega_{L} t\right\}-\frac{2A}{7 \pi}\cos\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}+7\omega_{L}
t\right\} +\cdots \end{eqnarray} \tag{11} \]
ここで、
\[ \omega_{L}=\omega_{c} \tag{12} \]
とすると、(11)は
\[ \begin{eqnarray} S_{I} \left( t \right)=
\frac{2A}{\pi}\cos\left(\omega_{d}\left(t\right)t+\theta_{c} \right)+\frac{2A}{\pi}\cos\left\{\left(2 \omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c} \right\} \\ -\frac{2A}{3
\pi}\cos\left\{\left(-2\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c} \right\}-\frac{2A}{3 \pi}\cos\left\{\left(4\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c} \right\} \\
+\frac{2A}{5 \pi}\cos\left\{\left(-4\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c} \right\}+\frac{2A}{5 \pi}\cos\left\{\left(6\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c} \right\}
\\ -\frac{2A}{7 \pi}\cos\left\{\left(-6\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c} \right\}-\frac{2A}{7 \pi}\cos\left\{\left(8\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}
\right\} +\cdots \end{eqnarray} \tag{13} \]
となり、これにLPFを適用すると、
\[ S_{I} \left( t \right)= \frac{2A}{\pi}\cos\left(\omega_{d}\left(t\right)t+\theta_{c}
\right) \tag{14} \]
同様に入力信号にQ復調局発を乗じて、LPFを適用すると、
\[ S_{Q} \left( t \right)=
-\frac{2A}{\pi}\sin\left(\omega_{d}\left(t\right)t+\theta_{c} \right) \tag{15} \]
で、局発を正弦波とした場合と、同じ形の式になるので、
局発はパルスでも良い、、、という結論。
こんなにねちっこくやる必要があったのか?

コメントをお書きください