正弦波はパルスに比べると作るのが面倒です。直交復調の局発はパルスでもいい、、、ってなると、いろいろラクができます。結論から行くとパルスでもいいはずで、その理由を考えてみます、、、実験したほうが早い、、、のですが。
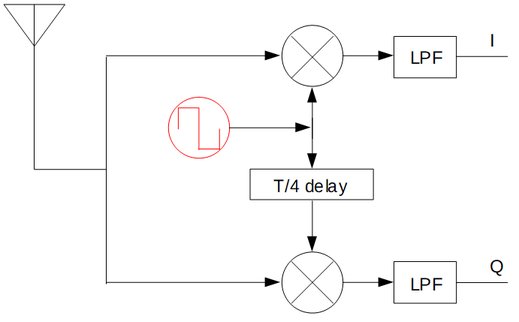
入力信号を
\[ S\left(t\right) = A \cos
\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}\right\} \tag{1} \]
とする(FSK)。
局発は

である。
ここで、矩形波のフーリエ級数展開を考える。
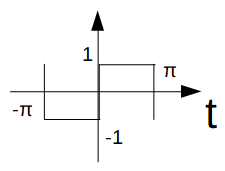
\[ \begin{eqnarray} f\left(t\right) = \begin{cases} -1 & ( -\pi \leqq t \lt 0 ) \\
1 & ( 0 \leqq t \lt \pi ) \end{cases} \end{eqnarray} \tag{2} \]
この矩形波のフーリエ級数展開は、下のようになる。(導出方法はあちこちに書いてあるので割愛)
\[ f\left(t\right) = \frac{4}{\pi} \displaystyle \sum_{n=1}^\infty \frac{ \sin \left\{
\left( 2n-1 \right) t \right\} }{2n-1} \tag{3} \]
これは周期がπの場合なので、周期をTにするため、tを2πt/Tに置き換える。
、、、意外とこのこたえを直接示してくれているサイトが見つからなかったので、自力で考えてみる。

コメントをお書きください