numpy  ·  16日 7月 2020

    CPFSKのスペクトラムを見る-続きというかMSKについて-

    wikipediaの「デジタル変調」によると、

    MSKは

    となりあうシンボルに対応する搬送波位相偏移が丁度90度（π/2シフトBPSKと同じ）になる

    らしいので、それを手掛かりにTを探る。

    FSKではコンスタレーションダイアグラムで一定の半径の円を描き、反時計回りに動くか、時計回りに動くか、がシンボルを示しているので、最も移動が小さくなるのはシンボルが1,0,1,0,1,...のような場合なので、その条件で解析する。

    評価用ソース

    波形生成

    fsk_study_gen.py

    1. # 変数クリア
    2. from IPython import get_ipython
    3. get_ipython().magic('reset -sf')
    4.  
    5. import matplotlib.pyplot as plt
    6. import numpy as np
    7. import scipy.signal as signal
    8.  
    9. # シンボル列を引き延ばす
    10. def extend_symbol_to_simulation_sampling_rate(symbols,t_symbol,t_simulation_sampling):
    11.     # シンボル数
    12.     size_of_symbols=symbols.size
    13.     # 最後のシンボルが終わる時間
    14.     end_time=size_of_symbols*t_symbol
    15.     # 計算タイミング
    16.     t=np.arange(0,end_time,t_simulation_sampling)
    17.     # 各シンボルの開始（終了）時間
    18.     t_periods_of_symbols=np.append(0,np.arange(1,size_of_symbols,1)*t_symbol)
    19.     # 結果データ領域確保
    20.     ex_symbols=np.zeros_like(t)
    21.     # 先頭データは入れておく
    22.     ex_symbols[0]=symbols[0]
    23.     # 各シンボルについて、その期間のインデックスを取得し、データを入れ込む
    24.     for i in range(0,size_of_symbols):
    25.         ex_symbols[np.where(t>t_periods_of_symbols[i])]=symbols[i]
    26.     return ex_symbols,end_time
    27.          
    28. # よく使う変数
    29. pi=np.pi
    30. deg2rad=pi/180.0
    31. twopi=2*pi
    32.  
    33. # 設定
    34. f_carrier=433.92e6            # 搬送波周波数 in Hz
    35. f_deviation=1e6         # 周波数偏差 in Hz
    36. f_sym=1e6                 # シンボルレート in Hz
    37. f_samp_simulation=f_carrier*10     # 計算のサンプリングレート in Hz
    38. phase_initial=0*deg2rad  # 搬送波の初期位相(何でもいい) in rad
    39. symbols_in_base=signal.max_len_seq(7)[0] # シンボル
    40. symbols_in_base[0::2]=1
    41. symbols_in_base[1::2]=0
    42.  
    43. # 後で使う変数
    44. t_sym=1/f_sym
    45. t_samp_simulation=1/f_samp_simulation
    46. omega_carrier=twopi*f_carrier
    47. omega_deviation=twopi*f_deviation
    48.  
    49. # シンボルを計算用に拡張
    50. [symbols,t_end]=extend_symbol_to_simulation_sampling_rate(symbols_in_base,t_sym,t_samp_simulation)
    51. symbols=symbols*2-1 # -1 or +1 にする
    52.  
    53. # 計算するタイミング
    54. t=np.arange(0,t_end,t_samp_simulation)
    55.  
    56. # 全計算タイミングにおける瞬間的な角速度
    57. omega_in_moment=omega_carrier+omega_deviation*symbols
    58.  
    59. # 全計算タイミングにおける瞬間的な位相変化量
    60. phase_change_in_moment=omega_in_moment*t_samp_simulation
    61.  
    62. # 全計算タイミングでの位相
    63. phase_t=np.cumsum(phase_change_in_moment)+phase_initial
    64.  
    65. # 波形生成
    66. amp_t=np.exp(1j*phase_t)
    67.  
    68. np.save('output/fsk_o_t',t)
    69. np.save('output/fsk_o_amp_t',amp_t)
    70. np.save('output/fsk_o_f_sym',f_sym)

     

    解析用ソース

    fsk_study_qdemod.py

    1. # 変数クリア
    2. from IPython import get_ipython
    3. get_ipython().magic('reset -sf')
    4.  
    5. import matplotlib.pyplot as plt
    6. import numpy as np
    7. from scipy import signal
    8.  
    9. # よく使う変数
    10. pi=np.pi
    11. deg2rad=pi/180.0
    12. twopi=2*pi
    13.  
    14. # 設定
    15. f_Lo=433.92e6            # 搬送波周波数 in Hz
    16. f_samp_simulation=f_Lo*10 # 計算のサンプリングレート in Hz
    17. phase_Lo=0*deg2rad    # 搬送波の初期位相(何でもいい) in rad
    18.  
    19. # 後で使う変数
    20. t_samp_simulation=1/f_samp_simulation
    21. omega_Lo=twopi*f_Lo
    22.  
    23. # 波形を読み込む
    24. t=np.load('output/fsk_o_t.npy')
    25. amp_t=np.load('output/fsk_o_amp_t.npy')
    26. f_sym=np.load("output/fsk_o_f_sym.npy")
    27. t_sym=1/f_sym
    28.  
    29. # 局発信号の生成
    30. amp_LoI_t=np.cos(omega_Lo*t+phase_Lo)
    31. amp_LoQ_t=np.sin(omega_Lo*t+phase_Lo)
    32.  
    33. # ミキサー
    34. amp_I_t_before_LPF=amp_t*amp_LoI_t
    35. amp_Q_t_before_LPF=amp_t*amp_LoQ_t
    36.  
    37. # フィルター係数生成
    38. freq_cutoff=10e6
    39. w_cutoff=freq_cutoff/(f_samp_simulation/2)
    40. b,a=signal.butter(1,w_cutoff,'lowpass')
    41.  
    42. # フィルター適用
    43. amp_I_t=signal.lfilter(b,a,amp_I_t_before_LPF)
    44. amp_Q_t=signal.lfilter(b,a,amp_Q_t_before_LPF)
    45.  
    46. # プロット
    47. fig=plt.figure()
    48. ax=fig.add_subplot(1,1,1)
    49. plt.plot(amp_I_t,amp_Q_t)
    50. plt.xlim(-0.5,0.5)
    51. plt.ylim(-0.5,0.5)
    52. ax.set_aspect('equal', adjustable='box')

     

    シンボルレート一定で、コンスタレーションダイアグラムが90°で行ったり来たりするfdevのときにMSKということだろう。

    結果：

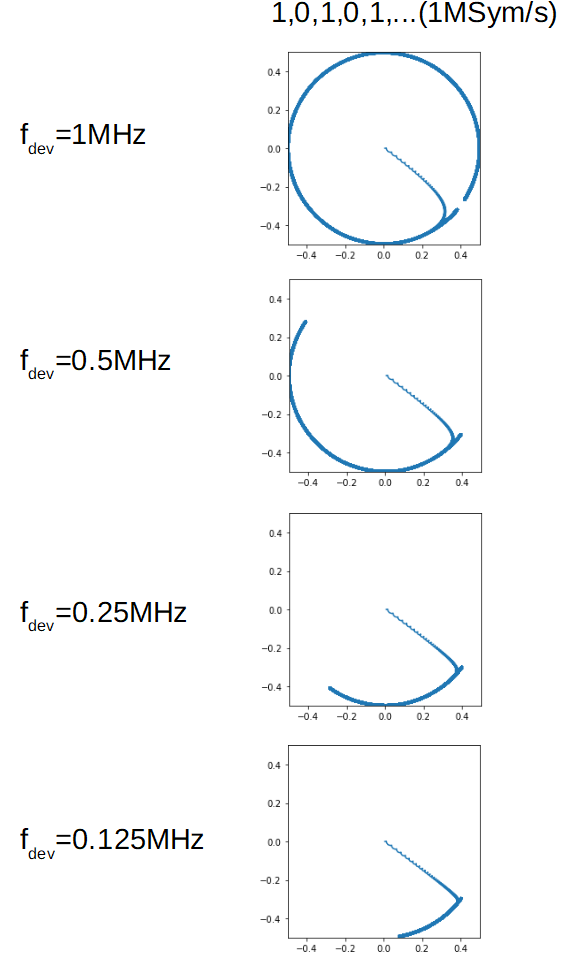
    ということは、fdev=0.25MHzでMSK

    \[m＝\vert f_{1}－f_{2} \vert T\] \[ \vert f_{1}-f_{2} \vert = f_{dev} \times 2 = 0.5MHz \] \[ T=\frac{0.5}{0.5MHz}=1\mu s\]

    ということで、Tはシンボルレートの逆数。

    カテゴリ： 非現実