ASKのスペクトラムを見る

1. # 変数クリア
2. from IPython import get_ipython
3. get_ipython().magic('reset -sf')
4.  
5. import matplotlib.pyplot as plt
6. import numpy as np
7. import scipy.signal as signal
8.  
9. # よく使う変数
10. pi=np.pi
11. deg2rad=pi/180.0
12. twopi=2*pi
13.  
14. # 設定
15. f_carrier=433.92e6            # 搬送波周波数 in Hz
16. f_sym=1e6                 # シンボルレート in Hz
17. f_samp_simulation=f_carrier*10     # 計算のサンプリングレート in Hz
18.  
19. # 後で使う変数
20. t_sym=1/f_sym
21. t_samp_simulation=1/f_samp_simulation
22. omega_carrier=twopi*f_carrier
23.  
24. # 生成して保存しておいた波形を読み出し
25. t=np.load('output/ask_o_t.npy')
26. amp_t=np.load('output/ask_o_amp_t.npy')
27. number_of_samples=t.size
28.  
29. # fftする
30. amp_f=np.fft.fft(amp_t)/(number_of_samples/2)
31. amp_f=20*np.log10(np.abs(amp_f)) #1Vrmsを0dBとしてdB表示(になっているんじゃないかと思う)
32. freq=np.fft.fftfreq(number_of_samples,t_samp_simulation)
33.  
34. # プロット
35. fig=plt.figure()
36. fig.add_subplot(2,1,1)
37. plt.plot(freq[0:int(number_of_samples/2)]/1e6,amp_f[0:int(number_of_samples/2)])
38. plt.xlim(f_carrier*0.995/1e6,f_carrier*1.005/1e6)
39. plt.ylim(-50,0)

ASK波形生成時に

1. symbols_in_base[0::2]=1
2. symbols_in_base[1::2]=0

として、

1,0,1,0,1,...

というコードで生成した場合。

433.92+/-0.5MHz, +/-1.5MHz, +/-2.5MHz, ...にピークが出ます。1MSym/sで1,0,1,0,1,...なのでシンボル周期が0.5MHzだから...

周期Tの矩形波をフーリエ級数展開すると

f, 3f, 5f, 7f, ... (f=1/T)

の成分があって、あとは三角関数の積和の公式から...そうなるわな。

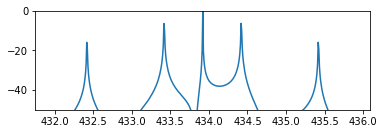
PN符号で生成した場合。

分散されます...そりゃそうだ。