せっかくCPFSK波形を作ったので直交復調してみたい。
その前に直交復調の計算について調べておく。
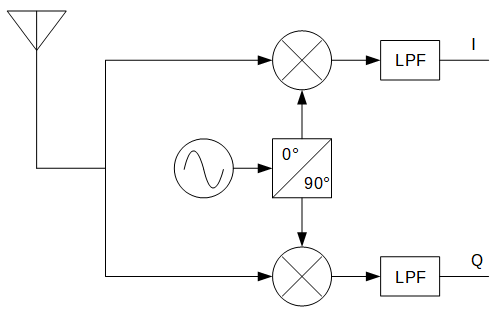
ということらしい。
なので、入力信号にcosωtをかけてLPFしたらI信号、sinωtをかけてLPFしたらQ信号。
局発周波数は入力信号がFSKの場合は、搬送波周波数と同じにするのが一般的らしい。
入力信号を
\[ S\left(t\right) = A \cos
\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}\right\} \tag{1} \]
とし、
局発信号を
\[ S_{LoI} \left(t \right) = \cos \left(\omega_{Lo}t+\theta_{Lo}\right) \tag{2} \]
\[ S_{LoQ} \left(t \right) = \sin \left(\omega_{Lo}t+\theta_{Lo}\right) \tag{3} \]
とする。
まずはI信号を計算してみる。入力信号に局発を乗ずればいいので、
\[ S_{I}\left(t\right)=S\left(t\right) \cdot S_{LoI} \left(t \right) \tag{4} \]
\[ S_{I}\left(t\right)=A \cos
\left\{\left(\omega_{c}+\omega_{d}\left(t\right)\right)t+\theta_{c}\right\} \cdot \cos \left(\omega_{Lo}t+\theta_{Lo}\right) \tag{5} \]
\[ S_{I}\left(t\right)= \frac{A}{2} \cos
\left\{\left(\omega_{c}+\omega_{d}\left(t\right)-\omega_{Lo}\right)t+\theta_{c}-\theta_{Lo}\right\} + \frac{A}{2} \cos
\left\{\left(\omega_{c}+\omega_{d}\left(t\right)+\omega_{Lo}\right)t+\theta_{c}+\theta_{Lo}\right\} \tag{6} \]
LPFを通すと、
\[ S_{I}\left(t\right)= \frac{A}{2} \cos
\left\{\left(\omega_{c}+\omega_{d}\left(t\right)-\omega_{Lo}\right)t+\theta_{c}-\theta_{Lo}\right\} \tag{7} \]
ここで、
\[ \omega_{c}=\omega_{Lo} \tag{8} \]
であり、また、
\[ \theta_{diff}=\theta_{c}-\theta_{Lo} \tag{9} \]
とすると、(7)は
\[ S_{I}\left(t\right)= \frac{A}{2} \cos \left(\omega_{d}\left(t\right) \cdot
t+\theta_{diff}\right) \tag{10} \]
と表せる。
同様にQ信号を計算すると、
\[ S_{Q}\left(t\right)= -\frac{A}{2} \sin \left(\omega_{d}\left(t\right) \cdot
t+\theta_{diff}\right) \tag{11} \]
(10)、(11)より、直交復調後の解析信号は
\[ S_{qd}\left(t\right)= \frac{A}{2} \exp^{-j \left(\omega_{d}\left(t\right) \cdot
t+\theta_{diff}\right)} \tag{12} \]
と、表せる。

コメントをお書きください